A Basis for Reimagining Chainmail
Chainmail is an interesting ruleset for mass combat as well as individual scale combat, but its rules are a bit disparate and convoluted. They can also be difficult to interface with the use of a Dungeons & Dragons campaign, where we might expect mass combat as well as individual combat against typical human-like beings or fantastic ones like dragons—all of which are given distinct subsystems in Chainmail.
This is my attempt at a unified system of Chainmail, working with the abstraction of the mass combat system as well as the relative simplicity of the one-versus-one combat system. This will entail initially an analysis of the mass combat system with respect to its likelihood of landing hits as well as to its implicit attack classification system. Then, I will discuss four methods to redesign Chainmail: by approximating mass combat in standard dice rolls (A&B); by using variable dice to represent types of units (C); and by simplifying the existing system to focus on ratios of relative unit or group strength (D). The first two retain the same math as the original game, but the last two have potential to unlock the same play style as the original mass combat system but with different emphases. Overall, I come to find that the needs of mass combat and one-versus-one combat may be distinct enough to warrant different treatments; yet that at least shouldn’t stop us from exploring different solutions for each of them.
Abbreviations include:
- LF: Light foot (infantry) unit
- HF: Heavy foot (infantry) unit
- AF: Armored foot (infantry) unit
- LH: Light horse (cavalry) unit
- MH: Medium horse (cavalry) unit
- HH: Heavy horse (cavalry) unit
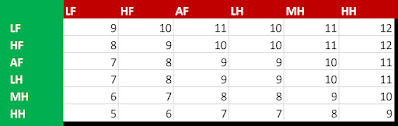
Chainmail Statistics
Above is a % chance likelihood of each unit landing a hit (vertical axis is attacker, horizontal is defender). Keep in mind that the actual minimum likelihood is 1-in-6, which is approximately 0.17. Units whose likelihoods are less than 0.17 represent units which must attack in numbers greater than 1 in order to land even a single hit against their opponent. For example, 4 light foot units must work as one in order to attempt to attack a heavy horse. Their likelihood is given therefore as 1-in-6 divided by 4, or 0.042. Overall, a unit attacking a unit of the same ability will have a 1-in-6 likelihood of defeating their target; meanwhile the maximum likelihood is 80%, and the minimum likelihood is 4%. Compare that to the one-versus-one table where, against an unarmored opponent, you often have a 58% chance of hitting.
Generally speaking, light horse is equal in capability to armored foot. However, light foot units treat light horse as heavy foot and medium horse as armored foot, meanwhile having an equal chance of defeating a heavy horse unit as a heavy foot does. This makes the light foot feel somewhat forgiving despite its otherwise lesser capabilities, in as much as they are not worse than heavy foot to the same degree that heavy foot is worse than armored food. Anyway, besides that exception, the armored foot and light horse seem to be equal in combat capability. This means we can consider there to really be five rather than six ranks of capability, which we can number 0-2 for foot soldiers and 2-4 for cavalry.
Alternatives
The first two solutions I offer here, 2d6 and 3d6, take after the one-versus-one combat system since they are easy to roll in the context of one unit attacking one other unit, but can be unwieldy with multiple attacking units (where each one rolls 2d6 or 3d6). The third “variable dice” solution takes more after the mass combat system, making it easy to represent multiple units attacking the same target, but requiring different kinds of dice. The last solution is a simplification of the original system based on ratios between different units and their relative strengths, avoiding both tedious attack rolls and weird dice, but introducing a level of overhead math.
Method A: 3d6 Approximation
This method is closest to the original in terms of likelihood. It is slightly more punishing towards power disparities, such as LF vs HH. See below:
- LF vs LF: 14 (16%)
- LF vs HH: 17 (2%)
- HH vs LF: 10 (63%)
To improve the performance of LF, we can decrease all target scores by 1 for the following results:
- LF vs LF: 13 (26%)
- LF vs HH: 16 (5%)
- HH vs LF: 9 (74%)
This method could also easily interface with different target numbers for certain weapons attacking certain kinds of armor, like in the original one-versus-one system, if desired. However, it complicates the resolution of a mass melee by rolling for each unit involved, rather than being able to weaker group units together to attack a single target.
Method B: 2d6 Approximation
This method is less accurate than A and has a smaller range of results, meaning we have to pick whether we want better chances of weak units versus strong ones, or if we want units to last longer in general like in the original. The scheme below has the following stats:
- LF vs LF: 9 (28%)
- LF vs HH: 12 (2%)
- HH vs LF: 5 (83%)
If we decrease the scores by 1, we get the following instead:
- LF vs LF: 8 (42%)
- LF vs HH: 11 (8%)
- HH vs LF: 4 (92%)
This system benefits from being extremely similar to the original one-versus-one system, being based on 2d6 rolls. However, like with method A, the one-attack-per-unit principle can slow down combat between weaker units and one stronger unit, which the original mass combat system would have handled by one roll for each “side”. At the same time, the increased likelihoods of defeating each unit can make combat faster and furiouser—which may be desirable for some!
Method C1: Unopposed Variable Dice
Let LF = d4, HF = d6, AF = d8, LH = d8, MH = d10, and HH = d12. An attacking unit can land a hit against its target by rolling its die greater than or equal to the highest possible roll of its target. For example, in order to land a hit against a unit of type HF, one must roll 6 or more. Units can attack as one in order to improve their likelihoods of success, by rolling all their dice together (for example, 3 units of type HF will roll 3d6 in a combined attack). Below are the base likelihoods of success for individual dice:
The minimum number of units to land a hit against another unit of a certain type is:
Like in the original Chainmail, it is thus necessary to attack in large groups in order to defeat stronger enemies. Although the number of units necessary to possibly land a hit in these cases is smaller, of course one’s chances are vastly improved when more units are brought into the fray.
One benefit of this method to A and B is that melee can be handled on the basis of many attackers versus one target, rather than each unit making one attack versus one target. This makes it easier to play as originally envisioned, but it does introduce a variety of die shapes which is not often desired.
This method also makes it easy to differentiate between a unit’s attack and defense capabilities. For example, take the dwarf who is defined as attacking as a unit of type HF but defends as a unit of type LF. We can represent this as a dwarf rolling d6 to hit, but falling on a roll of 4 or more.
Method C2: Opposed Variable Dice
This method uses the same definitions as before, except instead of using static target numbers for an attack, the target rolls their own die to determine if they are hit. For example, a unit of LF attacking a unit of HH is represented as rolling d4 versus a d12. This not only vastly improves a unit’s chance of landing a hit, but it also makes it possible for any one unit to land a hit against a stronger unit.
Although opposed variable dice greater adds randomness to an attack, it also makes it so that attackers and defenders roll at the same time to resolve one attack. This is undesirable for a simultaneous turn system where melees are resolved per conflict rather than per exchange of blows between two sides, as in standard D&D. Therefore unopposed rolls (C1) are better for war gaming style play, since they can be rolled at the same time, whereas opposed rolls (C2) may be more desirable for standard D&D style play where sides take turns resolving their actions.
Like before, this method can differentiate between a unit’s offensive and defensive capabilities. A dwarf would be defined as having d6 to attack and d4 to defend. However, the random defense means that it is more difficult to introduce greater complexity in the attack scheme, such as having different defense values versus different kinds of weapons. This is easy enough to imagine; here I am just working towards a basis.
Method D: Simplification
There are many expressions on the original mass combat table which, despite being computed in different ways, are ultimately statistically equivalent. We may benefit from simplifying the table to consolidate these expressions so that only the simpler ones are used, or taking a more radical approach by letting the stronger unit roll 1 die for each opposing (weaker) unit—for example, while 4 LF roll 1 die against 1 HH, that HH could roll 4 dice for each of its opponents. Consider the initial table below, based on this idea:
We can reword this to say that stronger units can always attack smaller units and succeed on a roll of 6, but weaker units can only counterattack by combining their numbers. Consider giving foot units values from 1 to 3, and cavalry units values 2-4. For example, 1 HH unit has a strength of 4 and so does 2 LF unit plus 1 HF unit. The former side would be able to attack each of the other units, but the latter side can only attack its opponent once.
A Little More Complexity
If the 1 HH were outnumbered by, say, 3 LF and 1 HF, it would be unfair for it not to be able to attack at all. We can rephrase the rule in terms of action points: it costs 1 point to attack 1 LF, 2 points to attack 1 HF, 3 points to attack 1 AF, and so on. 1 HH has 4 points to spend per turn, so it can attack 3 LF or 2 LF and 1 HF. Meanwhile, the opposing side has 5 total points, so it can only afford to attack its opponent once.
This solution has the benefit of only using six-sided dice and being able to handle proper mass combat. However, the math of comparing units’ relative strengths may be tedious even if the numbers are small. We can prevent tedium by limiting the melee to a circle of a 3” diameter, which fits about 5 units with 1” bases.
It also may interface in very interesting ways with hit dice. Consider that 1 HH is equal in strength to 4 LF; we can consider it as having the power of a hero, said to have 4 hit dice. Superheroes have 8 hit dice, and so may be said to have a relative strength of 8. Monsters have all kinds of hit dice values, ranging from the minute (0.5) to the massive (10), and these can be treated in the same way. Finally, similar to how monsters in Chainmail may have different offensive and defensive abilities, we can represent this by units having different point budgets and point costs. For example, a dwarf could have 2 points to spend (as HF), but could only cost 1 point to attack (as LF). In general, I think large monsters should have at most an attack cost of 4 points so that they can be attacked by hero units or by groups of slightly less powerful units.
Units may have, overall, four standard characteristics:
- ATK: Points to contribute in an offense.
- DEF: Point cost required to attack.
- MOV: Rate of movement per turn.
- SIZ: Size relative to a human being.
Most regular units have equal ATK and DEF, such as the original Chainmail units which we took as our basis (LF, HF, AF, LH, MH, HH), but as discussed it would add variety to have units with differing values for these two scores. Having units of differing size, such as dragons being larger than human beings, can help balance power disparity between massive versus smaller units (for example, a dragon may have ATK 8, but if it were the size of 3 humans then it could only attack 2 at a time in a melee). In order to maintain the rule that heroes can attack fantastic monsters of HD 4+, we may say that the maximum DEF score is 4 despite the HD of the creature; we may then associate DEF from 1 to 4 with no armor, leather armor, chain armor, and plate armor.
Bearing in mind the one-versus-one table, the DEF characteristic can be simply a qualitative armor class (none, leather, chain, plate) against which different weapons have different capabilities. The reduced scale from 8 armor classes to 4 would help facilitate this. However, not being able to attack an opponent without assistance could be sort of annoying—this is a case where we may prefer something like methods A, B, or C2 which are also the most similar to the original one-versus-one system.
Finally, this method is very similar in concept to the rules for ranged attacks, where masses of archers are required in order to land hits at increasingly strong or well-protected targets. This helps the ruleset feel cohesive and familiar.
Conclusion
I think methods C and D have the most potential for a renovation of Chainmail. Methods A and B, while being equivalent mathematically, discard the aspect of abstract and mass melee combat which makes Chainmail desirable as a ruleset. Method C affords us the abstraction of one die per unit, which is very convenient and simple to grasp, but it also requires a variety of dice types. Meanwhile, method D relies upon the ratio of strength between different units, which is a question of strategy central to Chainmail; and it also seems to interface well with the hit dice measure which has become standard in fantasy campaigns. My favorite, I think, is Method D for its fidelity to the original and its lack of weird dice. However, although strength in numbers makes sense for mass combat, it may pose a combat for one-versus-one combat. Maybe I shouldn’t be so hasty to combine the two modes.
At the same time though, seven people against a dragon? What would you expect to happen?






Comments
Post a Comment