chainmail one-on-one combat stats for weapons & armor

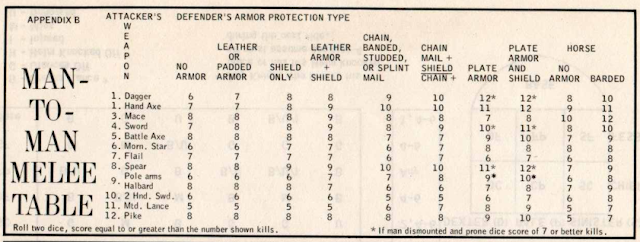
how useful is that big table in chainmail that lets you find your kill chance by comparing weapons to armor? you know, this one:

statistical analysis

let's see! first, i replicated the table in excel:

then i switched from scores to hit on 2d6 to % chance.

then, i compared the following categories:

• "light" armor: no armor (leather is almost always an improvement
• "medium" armor: average of chainmail and chainmail plus shield
• "heavy" armor: average of plate and plate plus shield

a positive number indicates that armor becomes more effective as it becomes heavier, whereas a negative number indicates that armor becomes less effective. for example, a battle axe becomes less effective between light and medium armor, but becomes more effective between light and heavy armor. in other words, it is specifically (slightly) more effective against chainmail than no armor at all.

since this table doesn't tell the whole story, since there's the caveat that a shield will either add +0 or +1 to a roll (i don't think there's rhyme or reason to it).

anyway, the most important column is the righthand one because it indicates whether the weapon might ignore armor. the following seem to:

• mace
• battle-axe
• flail
• 2-handed sword

and the following weapons are specifically effective against chainmail:

• battle axe
• flail
• 2-handed sword

ignoring the weapons which are especially effective against chainmail, here is the % chance of a blow hitting against a certain type of armor in increments of 5 (for use with d20):

• no armor: 60%
• leather: 55% (actually 60% because leather only helps against daggers & swords!) [+5%]
• shield: 50% [+10%]
• leather & shield: 45% [+15%]
• chain: 40% [+20%]
• chain & shield: 35% [+25%]
• plate: 35% [+25%]
• plate & shield: 25% [+35%]

and the % chance of being hit by a weapon without armor, also in increments of 5:

• dagger: 70%
• hand-axe: 60%
• mace*: 40%
• sword: 60%
• battle-axe**: 40%
• morning star: 70%
• flail**: 60%
• spear: 40%
• polearm: 70%
• 2-handed sword**: 70%
• mounted lance: 80%
• pike: 40%

* ignore armor
** ignores armor & effective against chainmail (perhaps by 15 to 20%?)

let's get into ways to translate this into a more intuitive system than looking at that awful table. keep in mind that there are some things that won't translate, like how daggers are actually very powerful against unarmored opponents but extremely weak against heavily armored ones, but for the most part this table is just noise with broad trends.

whitehack style, using 20-sided die

weapons have the following attack values, which is the value to roll below or equal to to land an attack:

• dagger: 14
• hand-axe: 12
• mace: 8
• sword: 12
• battle-axe: 8 (11 vs chainmail)
• morning star: 14
• flail: 12 (15 vs chainmail)
• spear: 8
• polearm: 14
• 2-handed sword: 14 (16 vs chainmail)
• mounted lance: 16
• pike: 8

weapons must also roll above the following armor values (not equal to):

• no armor: 0
• leather: 0 (2 versus swords and daggers)
• shield: 2
• leather & shield: 3
• chain: 4
• chain & shield: 5
• plate: 5
• plate & shield: 7

the following weapons ignore armor:

• mace
• battle-axe
• flail
• 2-handed sword

with rounder numbers for 20-sided die

attack values probably remain the same, but armor classes are as follows:

• no armor: 0
• leather: 2
• chain: 4
• plate: 6

where shield gives +1 to armor.

perhaps change attack values for the following weapons to be even numbers:

• battle-axe: 8 (12 vs chainmail)
• flail: 12 (16 vs chainmail)
• 2-handed sword: 14 (16 vs chainmail)

using two 6-sided dice

this is more natural lmao, since otherwise we're converting a bell curve to a bunch of increments of 5. this time let's just have ascending armor classes and weapons that give bonuses.

armor classes (?):

• no armor: 8
• leather: 8 (9 versus swords and daggers; apply in all cases if desired)
• shield: 9
• leather & shield: 10
• chain: 10
• chain & shield: 11
• plate: 11
• plate & shield: 12

weapon bonuses (add to initial score of 2-12):

• dagger: 2 (maybe only for unarmored or leather-armored foes, and 0 otherwise)
• hand-axe: 1
• mace*: 0
• sword: 1
• battle-axe**: 0
• morning star: 2
• flail**: 1
• spear: 0
• polearm: 2
• 2-handed sword**: 2
• mounted lance: 3 (should we assume this is just a polearm, and you get +1 when mounted?)
• pike: 0

* treat all armor as unarmored
** ignore armor and +1 vs chainmail

postscript on weapon reach

keep in mind that some following weapons have a pretty far reach, and that this is essential to playing the game strategically. it might still be worth having a value that indicates this ('weapon class' in the original chainmail), since it doesn't require a table or anything. or even just an indicator that says "this weapon reaches farther than others", but that doesn't account for much relative difference.

maybe short reach weapons:

• dagger
• hand-axe
• mace
• sword

medium reach weapons:

• battle-axe
• morning star
• flail
• spear
• 2-handed sword (it cannot be not that long--but count as so if you really want to)

long reach weapons:

• polearm
• lance (just a polearm?)
• pike

finally, maybe we can say melee weapons have four (or five?) attributes when abstracting the table this way:

• bonus to-hit: 0 to 3 (or 2 if being mounted is a separate quality?)
• reach: light, medium, long (perhaps also count as 0 to 2?)
• ignores armor: true, false
• effective vs chainmail: true, false
• +1 when mounted (?): true, false

........

edit: i messed up and didn't include the halberd, but here:

• attack value 8 for whitehack style
• bonus of 0 for 2d6 style
• ignores armor, it looks like